我们就加入一个能够使相位超前的高通电路环节来对其进行补偿，因为高通滤波器具有相位超前的特性， 我们就利用他的这个特性来进行补偿，从而解决振铃问题。下面我们就来看看吧。

　　在上一弹中，我们讲了振铃是如何产生的，以及如何去避免振铃的产生。这一弹我们要讲的这是运算放大电路中的相位补偿问题，振铃的产生就是由于相位的滞后导致的，我们这节讲的相位补偿同样也可以解决振铃的问题，上一节采用的是破坏反馈回路的低通环节来解决甚至避免振铃问题。而这一节我们采用相位补偿方式解决振铃问题，这样想，既然我们没法避免低通环节的产生，我们就加入一个能够使相位超前的高通电路环节来对其进行补偿，因为高通滤波器具有相位超前的特性， 我们就利用他的这个特性来进行补偿，从而解决振铃问题。下面我们就来看看吧。

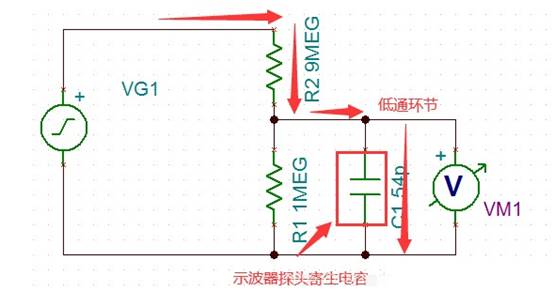
　　看下这种情况下的输出波形，由于低通环节的存在(积分电路)，导致输出波形圆头圆脑。

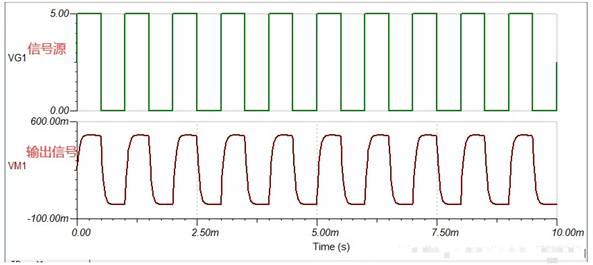
　　下面我们加入一个补偿环节来对电路进行补偿，这里我们在R2上并联一个电容，容值为6p,整好为54p的1/9，也即电阻比值的反比，至于为啥是这个比例，我们以后再作解释。今天记住就行。

　　这里先提前说下，针对当前的参数，补偿电容为6P时是处于完全补偿状态，小于6P则处于欠补偿状态，大于6P则处于过补偿状态。下面我们来看看电路仿真以及波形输出：

　　所以在选择补偿电容时一定要选择正确的参数，否则你的补偿电路可能会得不偿失。

　　采用上面相同的思路，我们同样也可以解决运放电路中振铃的问题。拿个电路出来

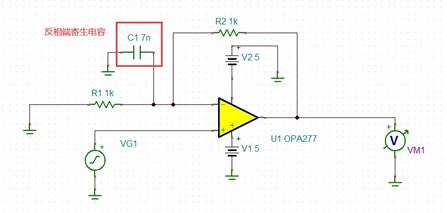
　　说明： R2和C1构成了一个低通滤波环节，使相位滞后，儿而我们在R2上并联一个电容C2,C2和R1构成一个高通滤波器，使相位超前，已达到相位补偿的作用。看图: